Flowability of Bulk Materials
Powder flowability guide ✓ Flow characteristics ✓ Flowability factor ✓ Cohesive materials ✓ Measurement methods ✓ Silo applications
Fundamentals
A Newtonian liquid is incompressible and transmits only compressive stresses at rest, not tensile stresses. The pressure in a liquid spreads equally in all directions. The ratio (λ) between horizontal and vertical pressure is one.
Stress ratio (λ) = horizontal pressure (σh) / vertical pressure (σv)
An ideally stiff solid, on the other hand, transmits tensile, compressive, and shear stresses. It deforms reversibly under load but does not flow; λ=0.
A bulk material transmits small tensile strengths, compressive and shear stresses at rest, and flows under the influence of sufficiently large shear stresses. A bulk material can behave like a liquid in a fluidized state or, in the other extreme, like a solid. Therefore, theoretically, stress ratios between horizontal (σh) and vertical pressure (σv) from 0<λ<1 are possible.
Characteristics of Bulk Materials
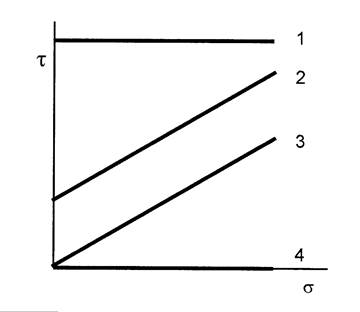
| Plastic bulk materials (1) |
φi=0 | Τc>0 |
| Cohesive bulk materials (2) |
φi>0 | Τc>0 |
| Cohesionless bulk materials (3) |
φi>0 | Τc=0 |
| Fluidized bulk materials (4) |
φi=0 | Τc=0 |
Ideal Plastic Bulk Materials (1)
(ΤC>0, φi=0)
 are incompressible. Their particles cannot change position due to saturation and usually have high cohesion. The contact surfaces remain constant despite changes in normal stress (σ), so the maximum occurring shear stress (τ) depends only on cohesion. Τ = ΤC. (e.g., saturated clay).
are incompressible. Their particles cannot change position due to saturation and usually have high cohesion. The contact surfaces remain constant despite changes in normal stress (σ), so the maximum occurring shear stress (τ) depends only on cohesion. Τ = ΤC. (e.g., saturated clay).
Due to their usually high cohesion, such materials are difficult to handle. Some samples only show plastic behavior at higher normal stresses.
Cohesive Bulk Materials (2)
(ΤC>0, φi>0)
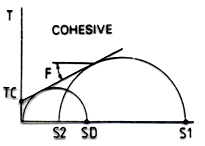 also have resistance to shear stresses (τ) due to interparticle contacts at a normal stress σ=0. Both frictional and cohesive forces occur in such bulk materials. These materials can be described by the equation Τ = σ * tan(φi) + ΤC.
also have resistance to shear stresses (τ) due to interparticle contacts at a normal stress σ=0. Both frictional and cohesive forces occur in such bulk materials. These materials can be described by the equation Τ = σ * tan(φi) + ΤC.
The rearrangement of particles in the static state is more or less restricted by cohesion, so previous compression by normal and shear stress as well as time consolidation influences later flow behavior. Therefore, the angle of repose depends on the history and can take different values. Simple measurement methods at or near bulk density ρb0 do not allow conclusions about storage and flow behavior under real conditions. To obtain qualified statements, measurements must always be carried out in shear testers where the flow behavior is measured under load.
By increasing the distance between particles in the flowing state, the influence of cohesion can largely disappear. Rearrangement of the particles is then possible again, and the previous packing density in the shear zone can change. Time consolidation can also be reversed.
In practice, this group of bulk materials is probably the most common. Depending on the flow properties, these materials are more or less difficult to handle. Accurate knowledge of the physical properties under operating conditions is essential and must always be measured. The variability of the materials must also be taken into account. Compressive strength can lead to bridging and thus to discharge problems if the hopper angle and outlet are not sufficiently dimensioned. The possible tendency to time consolidation should also be considered.
Cohesionless Bulk Materials (3)
(ΤC=0, φi>0)
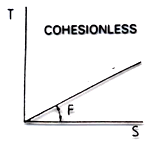 also known as free-flowing bulk materials, can be described by the linear equation τ=σ*tan(φi) (e.g., dry sand). The yield locus of such a material passes through the origin of the σ–τ diagram, and the internal friction angle (φi) corresponds to the angle of repose of the bulk material. The internal friction forces can vary for different materials but depend only on the current normal stress and not on the history.
also known as free-flowing bulk materials, can be described by the linear equation τ=σ*tan(φi) (e.g., dry sand). The yield locus of such a material passes through the origin of the σ–τ diagram, and the internal friction angle (φi) corresponds to the angle of repose of the bulk material. The internal friction forces can vary for different materials but depend only on the current normal stress and not on the history.
These bulk materials are usually easy to handle in practice. Due to the lack of compressive strength, bridging does not occur at the outlet (ideal cohesionless bulk material), and preloads are reversible. The bulk density at normal stress and the stress ratio should be determined for storage design.
Fluidized Bulk Materials (4)
(ΤC=0, φi=0)
are cohesionless due to their high particle distances and have no particle friction. In the fluidized state, bulk materials behave more like a liquid. Usually, the medium escapes again, more or less quickly, so that a non-fluidized state is restored. Especially fine, light substances tend to be fluidizable.
During handling and transport of bulk materials, such states can occur, for example, when mixed with air or other media, and can cause problems. This can lead to uncontrolled discharge through shut-off and conveying devices. Sufficient venting and storage time before further processing can prevent such problems. Special precautions must be taken during initial filling of systems, or sufficient residence time in storage must be ensured for adequate venting.
Professional Flowability Testing for Your Bulk Material
Benefit from our experience for precise flowability analyses and individual consulting.
- ✓ Over 30 years of experience
- ✓ Standard-compliant measurements
- ✓ Detailed evaluation reports
